
Computation is usually conceptualized in terms of input/output functions. For instance, to compute the square root of a number is to somehow solve the function that takes a number as an input and outputs its square root. It is commonly stated that feed-forward neural networks are “universal approximators” meaning that, in theory, any function can be approximated by a feed-forward neural network. Here are some examples of this idea being articulated:
“One of the most striking facts about [feed-forward] neural networks is that they can compute any function at all.”
– Neural Networks and Deep Learning, Ch. 4, Michael Nielsen
“In summary, a feed-forward network with a single layer is sufficient to represent any function [to an arbitrary degree of accuracy],…”
– Deep Learning (Section 6.4.1 Universal Approximation Properties and Depth), Ian Goodfellow
“…but can we solve anything? Can we stave off another neural winter coming from there being certain functions that we cannot approximate? Actually, yes. The problem of not being able to approximate some function is not going to come back.”
–Course on Deep Learning, Universal Approximation Theorem, Konrad Kording
More examples can be found here and here.
But it is not entirely accurate to say that feed-forward nets can compute any function. The universal approximation theorem places certain conditions on the types of functions it says are approximable. The target function needs to be continuous and defined over a compact subspace. The theorem does not cover functions that are non-continuous or defined over an open interval or over an infinitely-wide domain.
Now it might sound like I am being pedantic or taking statements out of context. In almost all these sources I linked above, they explicitly mention these conditions for the target function. However, implicit in their words is the assumption that these kinds of functions (continuous functions defined over a compact domain) are general enough to include any function we are practically interested in and can effectively compute. Perhaps the thinking is that non-continuous functions can be really strange and aren’t physical or practically useful. And the closed interval condition seems reasonable too. We don’t have infinite resources. So perhaps it makes sense to set aside functions that are defined over an infinitely long interval, or to select a bounded section of such functions to approximate.
Under this view, the problem is no longer to find a system that is expressive enough for general purpose computation, but rather to find the right parameters for a system we already have. We know a feed-forward network with the right parameters can solve any problem but how do we find one that does? In other words, the interesting question becomes how to learn. Given that there exists some network that does what you want, how do you find or build such a network? (This is why deep learning is significant. It provides an answer to this question).
Here, we need to take a step back and reconsider our implicit assumption. Is it really true that the kind of functions we are interested in and are able to compute are always continuous and defined over a compact domain? In reality, what kind of things can we compute with finite means? It turns out this question is a very old one. In the late 1930s a mathematician wrote a paper that began by asking: what kind of numbers/functions are – in Alan Turing’s words – “calculable by finite means”? This led to the conceptualization of a class of automatic machines that we today call Turing machines. (Ironically, many people today believe that Turing’s machines are infinite machines. The mistake here is to think Turing machines require an infinitely long memory tape. They don’t. They require an arbitrarily long memory tape. But this is too much of a diversion from our main discussion. You can read more about why Turing machines use finite means here).
While the universal approximation theorem applies to functions with closed bounded domains, the set of functions deemed to be computable [by finite means] include function defined over unbounded domains. For instance the problem of integer factorization is defined such that there is no limit to the size of the number fed as an input. Such a problem is solvable using python or C. There exists a computer program which – given sufficient finite resources (time, space, energy) – can factorize an integer of arbitrary size. Similarly, finite-state machines, which are weaker than Turing machines and programming languages but stronger than look-up tables, can solve problems with unbounded input size. There exists a finite-state machine which – given sufficient finite resources (time, energy) – can compute the remainder of any arbitrarily large number when divided by 7. Look-up tables on the other hand can only deal with functions defined over bounded domains.
But am I comparing apples to oranges? The types of functions studied in theory of computation appear to be string to string functions or integer to integer functions. The types of functions we approximate with feed-forward neural nets, on the other hand, are ℝ→ℝ functions that operate with real numbers. Is it even possible to compare computation power across these very different computation systems? Yes! Fortunately, people have come up with a rigorous framework for doing exactly that: comparing apples to oranges. (See https://doi.org/10.1093/jigpal/jzl003. The gist of it is that you can use a mapping between the input/output domains of one system to the other, e.g. from real numbers to strings, and that mapping has to be the same for both input and output domains. That allows you to compare computation power across different systems).
The idea behind the universal approximation theorem can be broken down into two parts (as nicely explained here and here):
- Look-up tables can be used to approximate any compact continuous function to an arbitrary degree of accuracy.
- Feed-forward neural nets can be used to appoximate any look-up table to an arbitrary degree of accuracy.
Therefore the level of computation power guaranteed by the universal approximation theorem is the same as that of look-up tables. It sounds much less impressive when you put it that way.
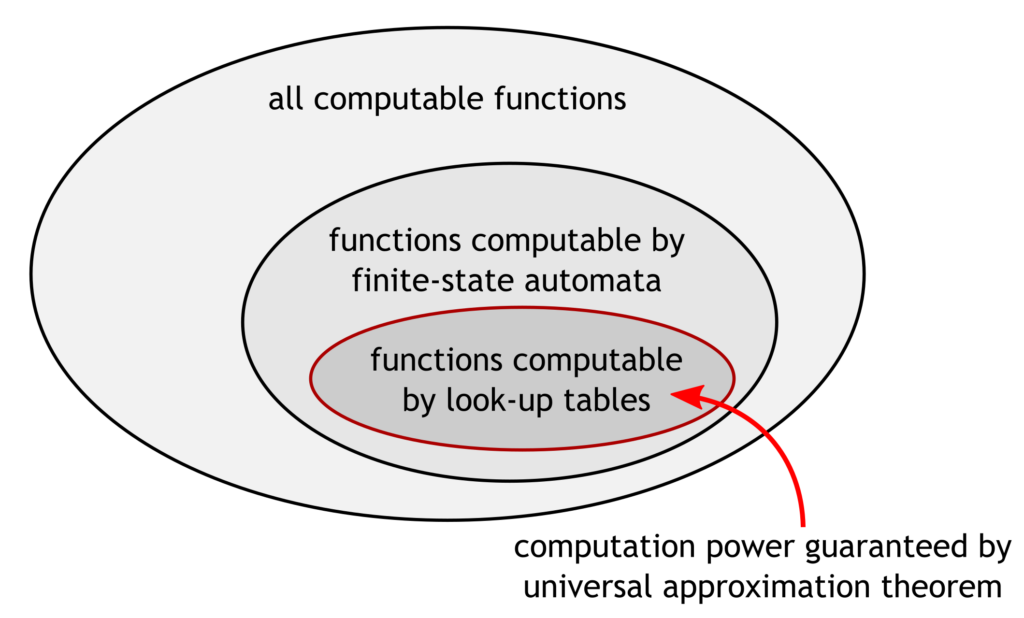
To clarify, this does not mean that feed-forward neural nets are proven to be as weak as look-up tables. It only means that the universal approximation theorem does not guarantee anything beyond the power of look-up tables. Someone might come up with some clever mapping between strings and real numbers that shows that they are more powerful than we think. (I highly doubt it, but I may be wrong!) I also haven’t said anything about recurrent neural networks here; the universal approximation theorem only talks about feed-forward neural nets with no memory.
The kinds of functions we are interested in for computation include things like integer factorization which work with unbounded domains. That is something that feed-forward neural nets – as far as we know – cannot deal with. Even if you think Turing machines are unrealistic abstractions (if you think this way I suggest you read this), I doubt you would deny that finite-state machines are realistic. Well, finite state machines are more powerful than look-up tables precisely because they can deal with unbounded input size (or an infinitely large input domain). It would be a strange disregard of computation theory to say the only realistic computing devices are look-up tables, or to say that look-up tables are “universal”.
In the fable of the emperor’s new clothes, after the child shouts out that the emperor is naked he continues walking through the town even more proudly than before. Exposing the king was not enough to overthrow him. But it may have swayed some of the townsfolk from exalting him.
