I will avoid an introduction and get straight to it. I’ll assume that you know what Turing-complete means, that you are familiar with transformers, and that you care about the question: Are transformers Turing-complete? (I may later write about what that question means and why it is important.)

Several papers claim that transformers are Turing-complete and therefore capable of computing any computable function. But I believe these claims are all misleading. Some make conceptual errors and are simply incorrect in their claims of Turing-completeness for their models. Others have modified the essential properties of transformers to achieve universal computation, presenting models that only resemble transformers superficially. As of October 2024, the deep learning model widely known as a ‘transformer’ (despite its success in commercial large language models) has not been shown to be Turing-complete (barring add-ons and modifications to its essential properties).

CORRECTION NOTE: In an earlier version of this post (April 22, 2023), I incorrectly stated that it is “easy to prove that transformers aren’t Turing-complete” because “any transformers can be simulated by a finite-state-machine”. That statement is false. My mistake was to assume that the maximum context window length was a limitation inherent to a specific transformer model. But I learned that there really is no maximum context window. The “width” of the model (usually “d_model”) has nothing to do with the number of tokens that a transformer can process. (I was fooled by how everyone calls the transformer a feed-forward neural network. But the attention layer in transformers isn’t quite a feed-forward neural network; it cannot be modeled with a fixed number of neurons and connections). A transformer can, in principle, process sequences of arbitrary length. It may not perform well beyond a certain length, but that’s a separate discussion about training and generalization. So you cannot simulate transformers with finite-state-machines. And since the model can store information in its growing sequence of tokens, this leaves open the possibility that transformers are, in fact, Turing-complete. I want to thank Nishanth Dikkala and Kevin Miller for bringing this mistake to my attention. In light of this realization, I have revised some of the critiques I brought up of specific papers.

---

Below, we’ll closely examine each paper that implies, or can be misinterpreted as claiming, that transformers are universal computers. In doing so, we will learn about the inner-workings of a transformer and understand what obstacles need to be overcome to create a machine learning model that learns functions within the scope of all computable functions.

Before we dive in, let me clear something up. My critiques below are not about hardware limitations or implementation. Some models rely on numerical values with arbitrary precision to ‘attend’ to tokens in the sequence. That’s fine. It’s common to use 64-bit floating point precision types, which are incapable of representing arbitrary precision values, but that’s an implementation choice separate from the abstract model of a transformer. In the same way that you can switch to a computer with more memory, you can always switch to higher fixed-precision to run a transformer on something that needs that extra boost to execute properly. You can even abandon the floating-point format altogether and store numbers as strings representing the numerator and denominator. As long as you don’t rely on infinite-precision, arbitrary finite precision is easily implementable in a digital representation scheme.

From the sixteen papers examined below, five incorrectly claim that their model is Turing-complete [1, 5, 10, 13, 14], eight present Turing-complete models which resemble transformers but operate in critically different ways, sometimes making them irrelevant to deep learning [1, 2, 3, 4, 8, 11, 12, 16], and three papers do not claim Turing-completeness but risk being misinterpreted as such [6, 9, 15]. (Categories are not mutually exclusive, and paper [7] does not even present a model).

In chronological order:

[1] Universal Transformers (2018)

Mostafa Dehghani, Stephan Gouws, Oriol Vinyals, Jakob Uszkoreit, Łukasz Kaiser

The authors provide an informal proof. “Given sufficient memory the Universal Transformer is computationally universal – i.e. it belongs to the class of models that can be used to simulate any Turing machine,… To show this, we can reduce a Neural GPU to a Universal Transformer. Ignoring the decoder and parameterizing the self-attention module, i.e. self-attention with the residual connection, to be the identity function, we assume the transition function to be a convolution. If we now set the total number of recurrent steps T to be equal to the input length, we obtain exactly a Neural GPU. Note that the last step is where the Universal Transformer crucially differs from the vanilla Transformer whose depth cannot scale dynamically with the size of the input“.

They refer to Neural GPUs Learn Algorithms (2018) that claims that Neural GPUs are universal because they can simulate 2D cellular automata. Now that paper also has an informal proof. And, as far as I can tell they are incorrect because the state of the Neural GPU during computation can be described by a fixed number of parameters. It is true that the number of parameters scales linearly with the input but it cannot recruit more parameters during computation. If you are familiar with theory of computation, one handy question to ask is: can the system run non-trivially non-halting patterns? Or can it go into enter a never ending path of computation that isn’t a obviously never ending and doesn’t repeat states? If it can’t then it’s not Turing-complete. The answer for Neural GPUs that attempt to simulate a 2D cellular automata is negative. Any never-ending pattern of computation in Neural GPUs will involve repeating states because the edges of the pattern are bounded and cannot expand during computation. Maybe Neural GPUs are only as powerful as a linearly-bounded automaton (a system which is less powerful than Turing machines but more powerful than finite state machines)? I don’t know, I’d like to see a formal proof. Nevertheless, their Neural GPU isn’t Turing-complete.

So the argument that “Universal Transformers” are Turing-complete because they can implement Neural GPU is flawed.

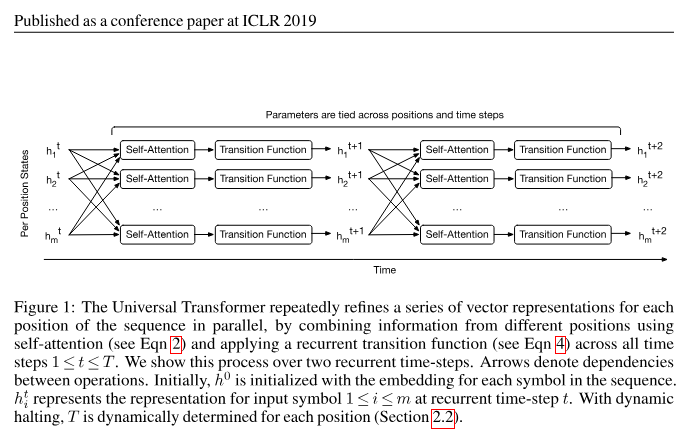
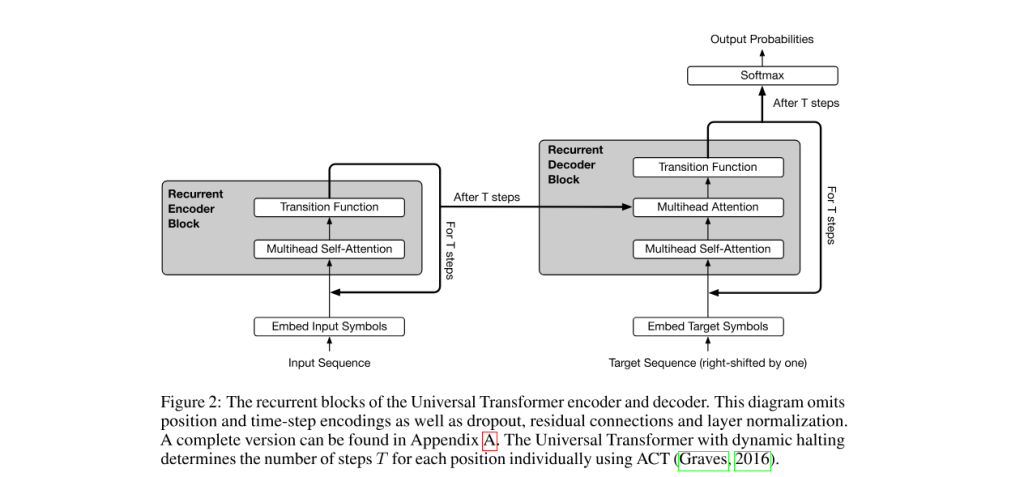
Apart from that, their model is—to their own admission—different from “vanilla” transformers which are used in large language models. While transformers normally have a fixed depth, their model can run an arbitrary number of layers for an input.

So it is neither Turing-complete nor is it the same transformer model used in LLMs today.

[2] On the Turing-Completeness of Modern Neural Network Architectures (2019)

Jorge Pérez, Javier Marinković, Pablo Barceló

The authors present two neural network models and show they are Turing-complete. Their proofs are correct as far as I can tell. The second model is a Neural GPU model and they prove Turing-completeness by showing that they can simulate any RNN, and RNNs with arbitrary precision are Turing-complete. (This is different from the proof of Neural GPUs Learn Algorithms that I described above, in that it uses arbitrary precision). I will not remark on their Neural GPU proof other than to say that it inherits the structurally instability of the Seegelman & Sontag 1992 RNN, hence, impossible to approximate or learn parameters for.

Now what about their transformer model? How do they prove Turing-completeness? To their credit, they actually show that given any Turing machine, you can simulate its behavior with a transformer-based model.

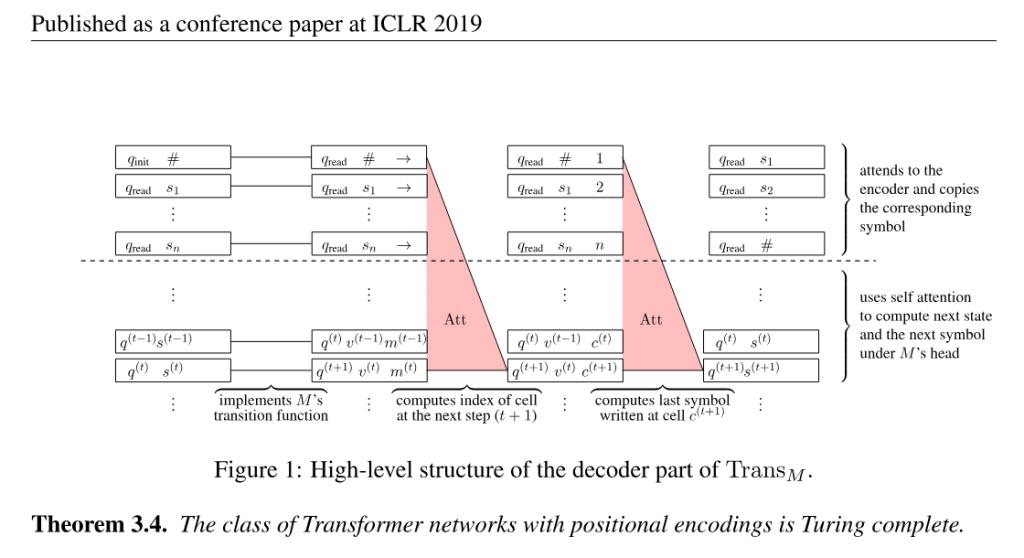
But to achieve universality, they sacrifice a number of fundamental properties of transformers: differentiability, structural stability, and [perhaps of least importance] a positional encoding scheme that doesn’t preserve consistent linear relationships between indices that are equally spaced apart. These issues arise for other papers below and I will only explain them once, here.

Computation in a Turing machine consists of discrete steps of reading a symbol, writing a symbol, and moving left/right. The way they simulate a Turing machine using a transformer is to store each event as a separate token in the sequence of tokens. With each full pass of information, the transformer generates a new token representing the next event of the simulated Turing machine. So the entire history of the Turing machine is spelled out in the growing sequence of tokens. Now, to produce tokens accurately, the model needs to figure out what the correct next step is. The main challenge here is to figure out a) where the tape head is located along the tape, and b) what symbol is written there. (The rest is easy; given these two pieces of information you can have a feed-forward network compute what direction to move in and what symbol to write). Okay, so how does it retrieve these two pieces of information from the sequence of tokens?

The trick is to use hard-max instead of soft-max in the attention layer. They use a version of the hardmax function that distributes evenly in the case of ties. So if there are r maximums, each one gets 1/r. You can use this feature to attend to all of the tokens in the history, average all the -1 and +1 values that correspond to left and right movements, and obtain the average movement so far. Then you multiply that by how many time steps have passed so far, which is encoded directly in the positional encoding of the current token (1/i where i is the current index in the sequence).

   

   

Once you have the current position of the Turing machine head, you can then “attend” to all the tokens corresponding to that position. You can pick the most recent one out because the positional encoding is strictly monotonic (1/i). With that you have the symbol that was most recently written into that position.

There are two major problems with this. The softmax function is a crucial feature of the transformer method that allows gradients to propagate through the attention layer during learning. Hardmax is a flat function. Its gradient is zero wherever the gradient is well-defined. You cannot find optimal parameters for it through gradient-descent and back-propagation will not pass through the attention layer. But perhaps more crucially, the model heavily relies on the tie case of their hardmax function. This makes the model extra brittle. The query×key values of all tokens must be exactly the same for that case to occur. An infinitesimally small change to the query or key values will radically disrupt the behavior of this model. So It is structurally unstable. That means that you cannot approximate its behavior as you gradually get closer to the target parameters during learning.

Another, albeit less severe, issue with their method lies in their positional encoding scheme. One of the main properties of positional encoding methods in transformers is that PE(i) can be transformed to PE(i+Δ) with the same linear transformation that only depends on Δ, independent of i. This allows a transformer to learn relationships between tokens regardless of where they occur in the sequence. This is the justification articulated in the original Transformer paper Attention is All You Need (2017).

One way to intuitively understand this is to think of positional encodings as multiple hands on a clock. Every hand rotates at a different constant speed. You can always shift to a new positional encoding by a rotation that is proportional to the size of the shift.

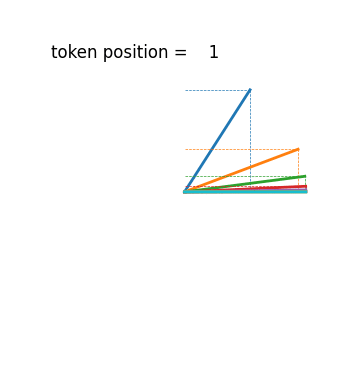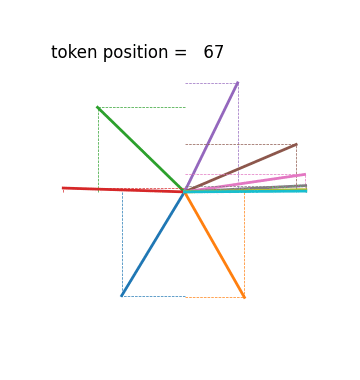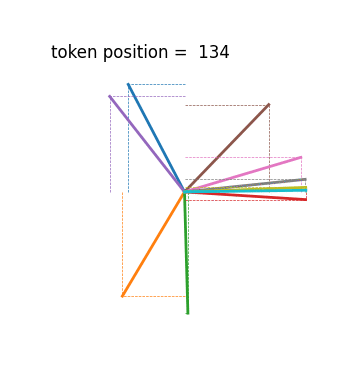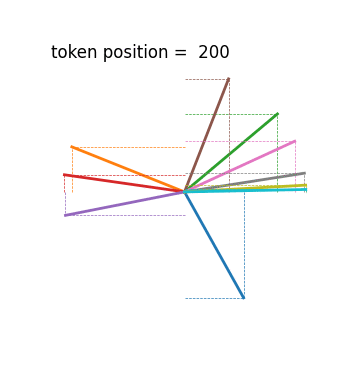
Their positional encoding PE(i)=1/i diverges from this strategy. I hesitate to say that they sacrifice an essential feature of transformers, since there are papers that claim transformers work without explicit positional encoding. But I do find it noteworthy and almost all of the different variants of positional encoding that are used today have the property described above.

The authors justify their choice of hardmax over softmax and 1/i over trigonometric functions by saying that they need to stick to rational numbers and that “softmax, sin and cos are not rational functions, and thus, are forbidden in our formalization”. An easy fix would be to replace Euler’s constant e with 2 or some other rational number, and to pick multiples of angles for which their sine and cosine values are rational, e.g. asin(3/5). However, I cannot see how they could have simulated a Turing machine with softmax and trigonometric positional encoding.

In summary, they present a model that is Turing-complete but deviates from transformer architectures in several critical ways and is, more importantly, not applicable to deep learning. Their model stores the entire history of the computation in the sequence of tokens, and retrieves information through a method that makes it structurally unstable (i.e. unable to withstand infinitesimally small changes in the model parameters). The parameters of such a model can never be discovered through gradient-descent based learning.

[3] On the Computational Power of Transformers and its Implications in Sequence Modeling (2020)

Satwik Bhattamishra, Arkil Patel, Navin Goyal

The authors present a Turing-complete model that resembles a transformer but is different in critical ways. There are two major problems with this model.

First, in there model, there is no vocabulary or “token” generation. The model takes as input a sequence of rational number vectors, and outputs a vector of rational numbers that gets appended to the sequence. This is in my opinion a major departure from transformer architecture, where the model outputs a probability vector and a token is chosen from that vector. It is true that tokens get converted to embedding vectors in transformers, but there should be a finite set of embedding vectors to select from. In their model, these vectors are free to take any value.

The second major problem is (similar to the previous paper) structural stability. We know that RNNs can simulate Turing Machines by treating the digits after the decimal point of a number as symbols on a tape Seegelman & Sontag 1992. However, structurally stable RNNs are not known to be universal (Moore 1998). So their model inherits the structural instability of Turing-complete RNNs. This is important because, again, the parameters of a structurally unstable model can never be discovered through gradient-descent based learning. There is no small enough neighborhood in parameter space where the model behavior resembles the intended dynamics. So this model is also Turing-complete, but deviates from transformer architectures in several critical ways and is, more importantly, not applicable to deep learning.

[4] Attention is Turing-Complete (2021)

Jorge Pérez, Pablo Barceló, Javier Marinkovic

To the best of my knowledge, this is exactly the same model as paper [2] above (from the same authors) and suffers from the same issues.

[5] Looped Transformers as Programmable Computers (2023)

Angeliki Giannou, Shashank Rajput, Jy-yong Sohn, Kangwook Lee, Jason D. Lee, Dimitris Papailiopoulos

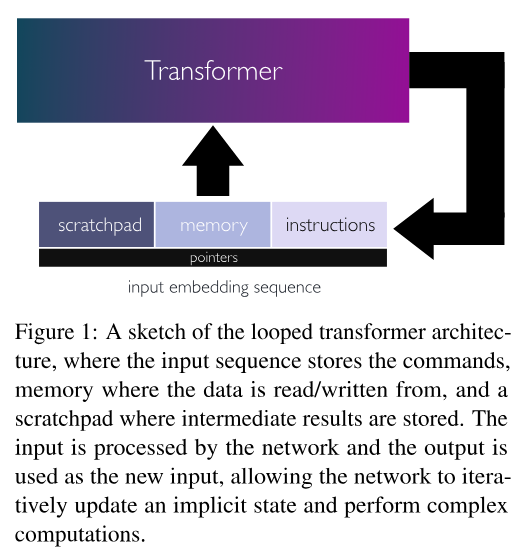
In this paper the authors present a model that they call “looped transformer”. Their model is essentially a transformer-like architecture that is fed a block of data, modifies that block of data, and then gets fed the data again. The crucial thing to notice about this model is that the size of the data is constant. There is no way to expand its size during computation. So unlike standard transformers that can store their state in an unbounded (yet finite) sequence of tokens, the looped transformer is much more limited.

The authors in this paper commit a conceptual error and are incorrect in claiming that their model is Turing-complete. Why? Because the state of the computation is stored in the matrix X and X has a size that is tied to the description of the transformer network. Their looped transformer can’t deal with an input of arbitrary dimensions. And since each entry in X can take one of a finite number of states, then X has a finite state space. So any looped transformer can be simulated by a finite state machine and is therefore not Turing-complete.

To show that a model is as powerful as Turing machines, one must show that for every Turing machine, there exists a configuration of that model that simulates that specific Turing machine. This can only work if the mechanics of the model are independent of memory resource constraints. They must be able to work with as much memory resources they are provided with. In a model with a fixed state spaces, like the looped transformer presented in this paper, there is no notion of adding memory resources without re-configuring the descriptor of the model.

[6] Statistically Meaningful Approximation: a Case Study on Approximating Turing Machines with Transformers (2023)

Colin Wei, Yining Chen, Tengyu Ma

In this paper the authors introduce a notion of approximating a computation system. They show that under their definition transformers can “statistically meaningfully approximate Turing machines with computation time bounded by T“. To quantify how well a transformer has approximated a function, they assume a probability distribution over the inputs Crucially T is tied to their transformer model size. (The number of parameters scales with T).

This paper does not claim that transformers are Turing-complete. But I think it is worth noting that it is not showing that they are “practically” Turing-complete either. What makes Turing-equivalent computation systems practical is that their configuration is specified independently from the resource constraints, and if a particular execution runs out of resources you can always add more resources without changing the logic of the program. (Read more here.)

A Turing-machine that can only run T steps can in theory be approximated – even fully solved – by a lookup table. The Turing machine cannot distinguish input sequences that are more than T symbols long. So one can list all the differentiable input prefixes, then simulate a Turing Machine for each one for T steps to obtain an output. And that completes a lookup table.

[7] GPT is becoming a Turing machine: Here are some ways to program it (2023)

Ana Jojic, Zhen Wang, Nebojsa Jojic

The authors claim that GPT-3 is “close” to becoming Turing-complete. I am not aware of such a notion of closeness to Turing-complete and they do not substantiate their claim.

[8] Memory Augmented Large Language Models are Computationally Universal (2023)

Dale Schuurmans

This paper demonstrates that one can simulate a Turing Machine through an LLM that can send commands to an external memory. The claim is correctly substantiated but it is worth noting that it does not demonstrate (nor does it claim to demonstrate) Turing-completeness of LLMs themselves. (Note that the same argument can be made about finite state machines. Finite state machine with access to an external memory tape are Turing-complete.)

[9] Sumformer: Universal Approximation for Efficient Transformers (2023)

Silas Alberti, Niclas Dern, Laura Thesing, Gitta Kutyniok

This paper does not demonstrate (nor claims to demonstrate) universal computation. I only list it because it is common to confuse universal approximation with universal computation, which are very different levels of computation power.

[10] Simulation of Graph Algorithms with Looped Transformers (2024)

Artur Back de Luca, Kimon Fountoulakis

The authors present a “looped transformer” model very similar to Giannou et al. 2023. Toward the end of their paper they claim that it is Turing-complete using a similar proof. But it suffers from the same conceptual error. The fact that the size of the data matrix is fixed and tied to the description of the transformer, makes it simulatable by a finite state machine. It is therefore not Turing-complete.

[11] The Expressive Power of Transformers with Chain of Thought (2024)

William Merrill, Ashish Sabharwal

The authors present a model very similar to the transformer-looking model in Pérez et al. 2019, with the same hardmax attention mechanism that precludes gradient-descent learning and relies on averaging on ties which makes the model structurally unstable. Refer to the explanation of paper [2] above. The only important difference is that it doesn’t need an explicit the PE(i)=1/i positional encoding and instead computes 1/i at every step by using the averaging on ties case for hardmax. This model is now doubly reliant on the tie condition of hardmax and this is problematic for the same reasons explained for paper [2].

[12] How Powerful are Decoder-Only Transformer Neural Models? (2024)

Jesse Roberts

The author presents a model very similar to Bhattamishra et al. 2020. See explanation on paper [3]. The model abandons the notion of discrete tokens from finite vocabulary and instead uses a sequence of vectors. A single vector can contain unbounded (yet finite) information through unbounded precision. That is the only way to simulate the Turing-complete RNN presented in Seegelman & Sontag 1992.

So, like paper [3], it deviates from a transformer by abandoning the notion of discrete tokens from a finite vocabulary, and also lacks structural stability which makes the parameters of that model unlearnable.

[13] Universal Length Generalization with Turing Programs (2024)

Kaiying Hou, David Brandfonbrener, Sham Kakade, Samy Jelassi, Eran Malach

The authors present a transformer based model that simulates a Turing machine through what they call a “Turing program scratchpad strategy”. They claim to that transformers can simulate any arbitrary Turing machine.

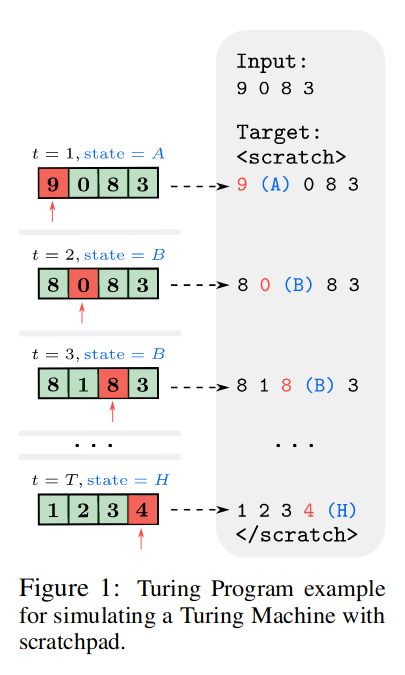
In this model the transformer produces tokens that compose a text scratchpad consisting of a full representation of the entire tape for every step. And this gets repeated for every step, storing snapshots of the entire history of computation.

They use Hard-ALiBi positional encoding which makes it possible to attend to tokens that are at maximum m tokens away from the current token. The value m can be different for different attention heads, but it is possible for m to be equal to infinity for some heads so that the transformer isn’t totally blind outside of a certain window size, but that infinitely-wide attention head will be indifferent to the order of tokens.

The problem here is that the model can only simulate a Turing machine with a fixed tape size. There is no way to extend the tape length when the ends are reached. Note that in order to properly simulate a Turing machine, one does not need an infinitely long tape, but rather an extendable finite tape. The state of the Turing machine is describable by a finite length string at any point of its computation. (As Marvin Minsky once said “instead of an infinite tape, we need only an inexhaustible tape factory” and that “this picture gives a reassuringly finite picture [of Turing machines]“).

One useful rule of thumb when evaluating the Turing-completeness of a mathematical system is to ask: can I describe that system by a finite length string? Does that string have a fixed length? If the answer to both questions is “yes”, then it can be simulated by a finite state machine and hence is not Turing-complete. If, on the other hand, the length of the description of the string can grow during computation, then it might have a chance of being Turing-complete. A transformer model is generally the latter case due to the unbounded, yet finite, sequence of tokens that can store a computation state. But in this case, since the transformer attempts to simulate what they call a “Turing program scratchpad”, which has a fixed size description, it cannot be universal.

So this model is in fact, not Turing-complete, and cannot simulate an arbitrary Turing machine.

[14] Auto-Regressive Next-Token Predictors are Universal Learners (2024)

Eran Malach

This paper states: “We show that even linear predictors—models where the next-token probability is a linear function of the input sequence—are already powerful enough to compute any Turing computable function.” and that “For any function f that can be efficiently computed using a Turing machine, there exists a dataset D such that training a (linear) next-token predictor on D results in a predictor that approximates f.“

This is a much stronger claim, not just about the expressive power of next-token predictors, but also about learnability. But it is incorrect and stems from a conceptual misunderstanding about computability. The error occurs at this excerpt of the paper:

What is essentially being argued here is that auto-regressive token generators are capable of solving any function where the input size is fixed length. So they are as powerful as lookup tables (which can solve any {0, 1}^n -> {0, 1} function). And since a Turing machine with a runtime limit T can only distinguishBy the standards of this paper, lookup tables are capable of computing any Turing computable function, because any lookup table can store all the possible results for running a specific Turing machine up to T steps. But lookup tables are even weaker than finite state machines, let alone Turing machines. (This is similar to the error in paper [6], Wei et al 2023).

[15] Transformers are Universal In-context Learners (2024)

Takashi Furuya, Maarten V. de Hoop, Gabriel Peyré

This paper does not make any claims regarding universal computation/Turing-completeness. It uses the term “universal” in the sense of universal approximation theory, which does not guarantee universal computation. I only list it because it is likely to be misinterpreted by some readers.

[16] Autoregressive Large Language Models are Computationally Universal (2024)

Dale Schuurmans, Hanjun Dai, Francesco Zanini

The authors present an autoregressive token-generation model that is capable of simulating a universal Turing machine. Unlike how these models usually work, their model gets input from a sliding window (green below) that lags behind from the last tokens generated (red). Another critical feature of the model is that it can sometimes output two tokens instead of one. The ability to output two tokens is absolutely critical for universal computation because the only tokens that determine the behavior of the model are the ones that span between the sliding input window (green) to the end of the sequence. If that length is constant and unable to grow, then its behavior can be predicted by a finite state machine. If the model produces only one token at each step then that length stays constant. That is why they gave their model the capability to produce two tokens at once.

They show that using this setup you can achieve universal computation either through a simple deterministic auto-regressive language model (far simpler than a transformer), or through prompting a standard LLM with instructions on how to process the tokens. In the latter case, one must manually take the tokens in the sliding input window and concatenate it to the system prompt to then feed it to the LLM, at each step. So it is not as if the LLM would be able to do this on its own. It requires some external program that manages the sliding window, concatenates it to the system prompt, and appends the one or two output to the sequence that is kept hidden from the LLM. It is similar to [8] above (Memory Augmented Large Language Models are Computationally Universal 2023), except the external program is simpler here.

One side comment: They simulated a universal Turing machine (known as U_15,2) through 2,027 production rules. But if their goal was to demonstrate Turing-completeness, there is a much simpler way of doing it. Using their proposed lag system, you could easily simulate a universal linear cellular automaton, like Rule 110. They’d need two symbols for alive and dead cells and one symbol that marked the end of a pattern. Then with a sliding window of three symbols and special edge-case handling for extending the end of the pattern, you could simulate Rule 110 with only a handful of rules. I imagine engineering that prompt would have been much easier. Although, I do appreciate that they made new contributions relating lag systems to Turing machines.

So this system, while being Turing-complete, doesn’t say much about whether transformers or LLMs as we know them are Turing complete.

---

Conclusion

To show that transformers are as powerful as Turing-machines, one must show that given any Turing machine (or computer program), a single transformer exists that simulates it. What several papers [1, 5, 10, 13, 14] have done instead is to show that given a Turing machine and given the resource constraints on that machine there is a transformer that simulates it. This does not demonstrate Turing-completeness. Otherwise the notion of computation power becomes completely meaningless. Because by that standard, finite state machines are Turing-complete. You can simulate any Turing machine with a specified memory constraint using a corresponding finite state machine. Does anyone claim finite state machines are Turing-complete? And even lookup tables become Turing-complete, because you can catalog all the outputs of any Turing machine with a given runtime constraint. Under this framework all computation systems collapse into the same class.

Transformers have certain essential properties which make them relevant to deep learning approaches. Any specific transformer has a set of parameters that must be learned through gradient descent. In the standard design, the probability distribution of the next token is continuous with respect to those parameters. That means for an infinitesimally small change in parameters the output stays pretty much the same. (Additionally, we must be able to define a reasonable loss function that is differentiable with respect to those parameters). In several of the papers above, the do indeed present Turing-complete models [2, 3, 4, 11, 12] but they had to change the definition of a transformer such that it loses this essential property (e.g. they use hardmax instead of softmax and rely of the tie case of hardmax, or they throw out the vocabulary of tokens and simulate structurally unstable RNNs which are neither continuous nor differentiable).

Whether any of this matters for AI is a separate discussion. Some people might not care if our machine learning methods find solutions in languages that cannot express some computable functions. But I think universal computation is more important than ever for AI and that our progress is being hindered by ignoring it or watering down what it means to be universal.

Regardless of where you stand on this debate, universal computation is a rigorously well-defined concept. It is either true or false that the abstract model of a transformer is Turing-complete. When I say “transformer” I mean the system that is used in LLMs by any reasonable definition. Of course, there are acceptable variations to the design (e.g. different positional encoding methods, decoder only versions without cross-attention, stochastic vs. deterministic token generation). But a transformer has defining features that make it a transformer: It takes as input a arbitrary length sequence of tokens from a predefined vocabulary, generates one token at each step that gets appended to the sequence, uses attention layers with softmax such that the loss function is differentiable with respect to its parameters, and contains a fixed set of parameters with values that are unchanging during inference time. That is the model that everyone is using and has produced such impressive results that everyone is so excited about. It is not very informative to show that such a model can be made into a Turing-complete model with some modifications. A finite-state-machine can be made into a Turing-complete model with access to two stacks. But a finite-state-machine is still a finite-state-machine. All that being said, I cannot prove that transformers aren’t Turing-complete. Someone might actually come up with an ingenious solution that shows that transformers are, in fact, Turing-complete. But until then we should all be honest about the fact that no one has done so yet.

The feature image of this post was created using DreamStudio.